로봇의 각종 센서 정보를 통해 로봇의 위치를 추정하고 이동 경로 계획을 위한 SLAM을 하는 과정에서 센서를 통해 들어오는 정보에 잡음(노이즈)이 섞이는 경우가 발생한다. 이로 인해 추정된 위치 좌표가 실제 로봇의 위치와 다른 경우가 발생하는데 이러한 추정치를 보정하여 추정한 위치 좌표와 로봇의 실제 좌표와 일치시키는 알고리즘 중 하나인 칼만 필터를 소개하겠다.
칼만 필터(Kalman Filter)란?
칼만 필터는 잡음이 포함된 측정치를 바탕으로 선형 역학계의 상태를 추정하는 재귀 필터로 루돌프 칼만이 개발하였다.
칼만 필터는 물체의 측정값에 확률적인 오차가 포함되고, 또한 물체의 특정 시점에서의 상태는 이전 시점의 상태와 선형적인 관계를 가지고 있는 경우 적용이 용이하다. 또한 가우시안 분포에 효과적인 필터가 칼만 필터이다.
칼만 필터는 이전에 수집한 데이터가 다음 단계의 예측에 재사용되는 재귀 필터이기 때문에 해당 값들의 급격한 변화가 발생하는 비선형적인 상황에서 칼만 필터는 추정값의 범위가 커져 오차가 발생할 수 있다.
이러한 비선형 환경에서 적용할 수 있는 확장 칼만 필터(Extended Kalman Filter, EKF), 무향 칼만 필터(Unscented Kalman Filter, UKF) 등의 칼만 필터도 있다.

칼만 필터는 특정 시간(T)에 측정된 데이터로 다음 위치를 예측하는 예측(Prediction) 단계와 다음 측정(T + 1)에서 측정된 데이터와 예측한 값의 차이를 보상해 새로운 추정값을 계산하는 측정 업데이트(Measurement Update) 단계를 반복하는 재귀적 필터이다.
예측(Prediction) 단계
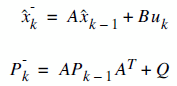
예측 단계에서는 이전 시간(T-1)에 측정된 데이터를 이용해 다음 시간(T)의 위치추정값을 예측하고 이전 시간(T-1)의 추정값이 얼마만큼 현재(T)의 추정값에 영향을 미칠 것인가를 나타내는 오차공분산을 예측한다.
행렬 A는 노이즈가 없을 때 위치추정값이 얼마만큼 T의 위치추정 결과값에 영향을 미칠것인가를 나타내는 공분산 행렬이다. 행렬 B는 사용자 입력에 의한 상태변화와 영향에 대한 보정 값이다.
예측한 값이 평균을 기준으로 어느 정도 분포되어 있는지 이전시간(T-1)의 오차공분산을 통해 다음시간(T)의 오차공분산 P를 예측한다.
측정 업데이트(Measurement Update) 단계

측정 업데이트 단계에서는 사전 추정값(예측값)과 오차 공분산, 칼만 이득 추정값을 바탕으로 추정값을 계산한 후 출력하며 오차 공분산을 업데이트 한다.
측정값과 예측값의 차이를 보상하기 위해 칼만 이득을 계산하는데 측정값이 노이즈에 수렴하면 칼만 이득의 계산식에 의해 칼만 이득은 커지게 되며 상태 추정 값의 계산에 칼만 이득 값이 많은 영향을 미치게 된다.
칼만 필터를 통해 측정 업데이트과정에서 구한 추정값과 오차공분산은 칼만 필터의 재귀적인 알고리즘에 의해 다시 실행될 때 다음 시간에 대한 위치 추정값을 구하는데 사용된다.
Reference.
성광현, 송충건, 유헌창. (2023). 엣지 컴퓨팅 환경에서 칼만 필터 기법 기반 거리 측정 센서의 보정. 한국컴퓨터교육학회 학술발표대회논문집, 27(1), 359-362.
박상욱. (2023). 칼만 필터 기반 지역 기온 추정을 위한 시공간 보강. 전자공학회논문지, 60(4), 65-70.
김대영, 박재완, 이칠우. (2013). CAMshift 기법과 칼만 필터를 결합한 객체 추적 시스템. 멀티미디어학회논문지, 16(5), 619-628.
윤성권. "UWB 통신 기반 실시간 3-D 위치추적 시스템 구현." 국내석사학위논문 한양대학교 대학원, 2022. 서울
'logistics' 카테고리의 다른 글
| 최적 경로 찾기 #3 - 벨만-포드(Bellman-Ford) 알고리즘 (0) | 2023.07.03 |
|---|---|
| [SLAM] 몬테카를로 위치 추정(Monte Carlo Localization)이란? (0) | 2023.06.27 |
| 로봇공학 입문 - 자유도란? (0) | 2023.06.26 |
| IMU센서와 센서 퓨전(Sensor Fusion) 기술 (0) | 2023.06.26 |
| SLAM이란? 무인 이동 차량의 지도 생성 (0) | 2023.06.22 |



