로봇공학 입문 - 자유도란?

로봇이 얼마나 자유롭게 움직일 수 있는가를 나타내는 자유도라는 개념에 대해 알아보겠다.

자유도를 이해하기 전에 공간을 나타내는 좌표계를 먼저 알아야 할 필요가 있다. 

좌표계는 보통 왼손 좌표계와 오른손 좌표계를 많이 사용한다. 좌표계는 로봇공학 뿐만 아닌 그래픽 업계, 게임 업계 등 공간을 적용해야 하는 곳에서는 어디든지 사용된다.

 

 

좌표계

왼손 좌표계에서 회전 방향은 각 축에 대해 시계방향으로 회전한다.

 

왼손 좌표계

 

오른손 좌표계에선 각 축에 대해 반시계방향으로 회전한다. 

오른손 좌표계

 

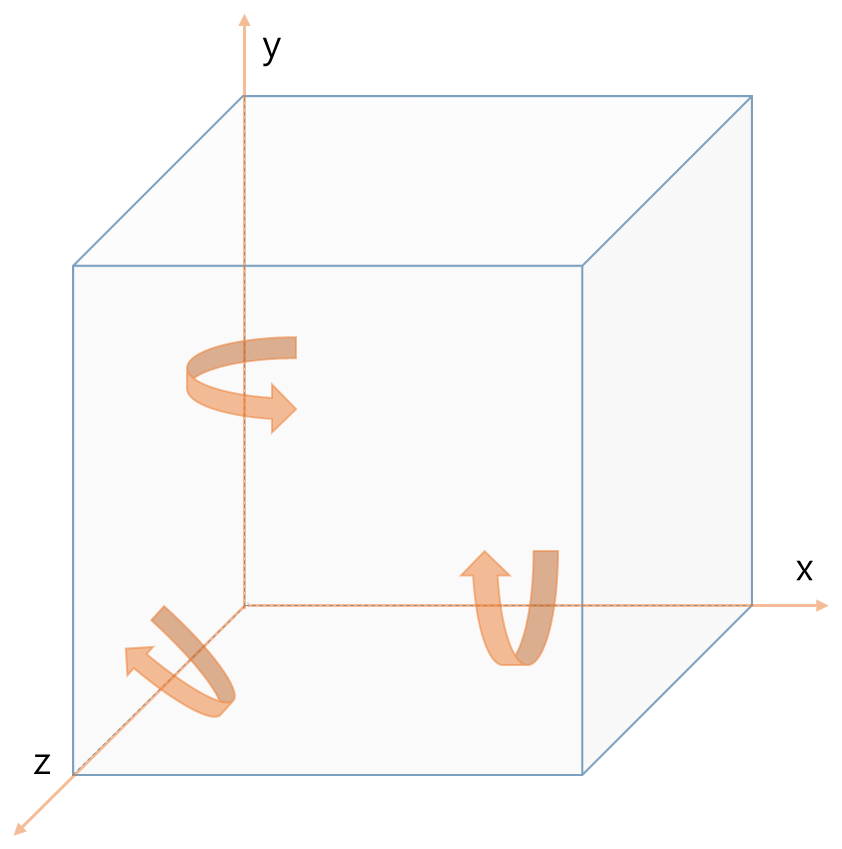
자유도(Degree of Freedom)

로봇공학에서 자유도는 로봇 구성에 필요한 실제 좌표의 최소 수라고 할 수 있다. 쉽게 말하면 로봇이 움직일 수 있는 경우의 최소 단위라고도 볼 수 있다. 즉. 자유도는 로봇의 위치와 자세를 결정하기 위해 필요한 변수들의 최소 갯수이다.

 

예를 들어 방문의 경우 방문의 자유도는 1이다. 문은 벽에 고정되어 있기 때문에 각도라는 변수 하나에 의해서 위치와 자세가 결정되기 때문이다.

동전의 경우 자유도는 3이다. x, y에 의해 동전의 위치가 결정되고 동전의 각도에 의해 동전의 자세가 결정되기 때문이다.

비행기나 드론의 경우 6자유도이다. 앞뒤(x축) 좌우(y축), 위아래(z축), x축의 회전, y축의 회전, z축의 회전으로 자세가 결정되기 때문이다.

 

3차원 공간에 원하는 위치에, 원하는 자세로 존재하기 위해 기본적으로 6자유도를 얘기한다. 6자유도는 3자유도보다 정교한 움직임이 가능하기 때문에 로봇공학 또는 산업용 로봇팔을 얘기할 때 6자유도가 많이 등장하는 이유이다.

6자유도는 위치(Position)를 나타내는 3자유도와 자세(Orientation)를 나타내는 3자유도로 나누어진다.

 

6자유도

• 서지(Surge) : 이동방향에  평행한 수평면에 대한 전후 운동
• 해브(Heave) : 이동방향에 수직의 수직면에 대한 상하 운동
• 서웨이(Sway) : 이동방향에 수직의 수평면에 대한 좌우 운동
• 피치(Pitch) : 이동방향에 수직의 수평면에 있는 축 주위의 회전
• 요(Yaw) : 이동방향에 수직의 수직면에 있는 축 주위의 회전
• 롤(Roll) : 이동방향에 평행한 수평면에 있는 축 주위의 회전

 

6축 로봇

6축 로봇은 보통 자유도를 높일 수 있는 관절(축)의 개수가 6개인 로봇을 6축 로봇이라고 칭한다.

 

출처. 두산 로보틱스

로봇의 축을 결정하는 방법은 다음과 같다.

• 회전이동(Rotational traverse)
• 방사이동(Radial traverse)
• 수직이동(Vertical traverse)
• 피치(Pitch)
• 요(Yaw)
• 롤(Roll)

 

Reference.

https://www.researchgate.net/figure/4-Roll-pitch-yaw-heave-sway-surge-of-a-ship_fig5_327838620

https://stementor.tistory.com/entry/%EB%A1%9C%EB%B4%87%EA%B3%B5%ED%95%99%EC%9E%85%EB%AC%B8-%EC%B2%AB%EB%B2%88%EC%A7%B8-%EC%9E%90%EC%9C%A0%EB%8F%84Degree-of-Freedom%EC%9D%98-%EA%B8%B0%EC%B4%88

https://blog.naver.com/cjsal95/220915601780

https://m.blog.naver.com/droneaje/221993443385

https://www.doosanrobotics.com/ko/News/NewsDetail/e11d7f75-72ae-e911-a848-000d3a07fd43

https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=jintaeky&logNo=221420290101